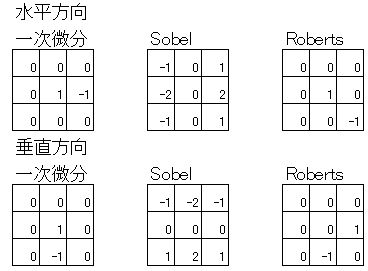
OpenCVに限らず、画像処理を勉強していると、Sobelフィルタ、Laplacianフィルタという言葉が出てきます。
一次微分フィルタ、二次微分フィルタの別名のような感じで記述されていることが多いですが、今後、いろいろなフィルタ処理を勉強するにあたって、その幾何学的な意味を確認しておいたほうがいいなと感じたので、まとめておきます。
画像処理におけるフィルタの意味
そもそも、フィルタ処理は、ComputerVisionの世界では、画像の中の特徴的な部分を抽出する手段の一つとして利用されます。
中でも、Sobel、Laplacian両フィルタは、画像の中の1画素に注目した場合、その画素が、その周りの画素と比較してどれほど異なっているのかの差分を捕らえることで特徴を抽出しようという差分フィルタの一種です。
つまり、下図のように f(i,j) → g(i,j) に変換する際、(i,j)(オレンジの部分)と、周りの画素(黄色の部分)との差分を新しくg(i,j)と定義することになります。
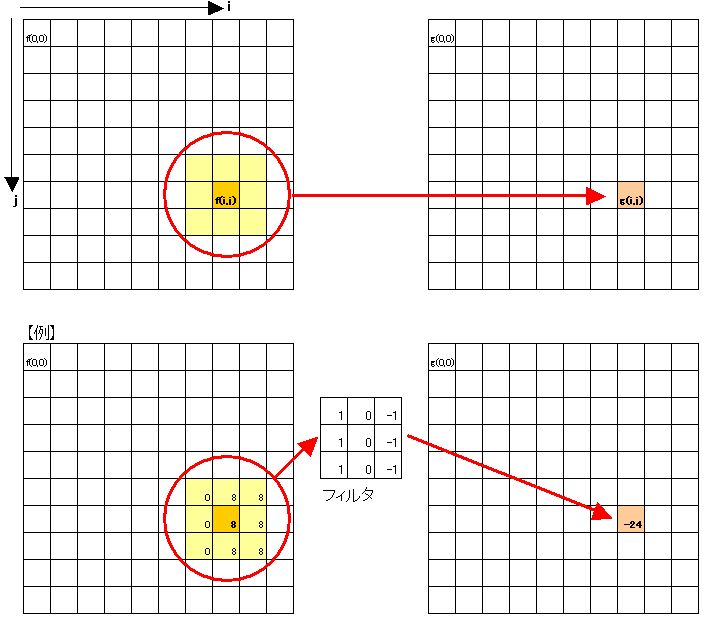
f(i,j) → g(i,j)の際に、画素のどの部分をその程度重み付けで考えるかで、変換後の値が変わってきます。それがフィルタです。
この【例】ではオレンジ色の画素ひとつについて着目しましたが、画像全体の画素についてこのフィルタを適用すると、以下のようになります。
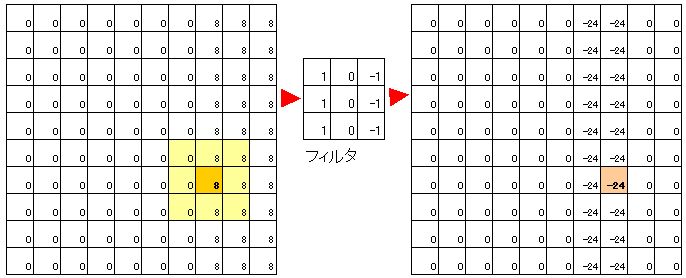
画素値の変化がX軸方向で起こっているところで、g(i,j)の値が急激に変化し、X軸方向の変化が無いところでは、0になっていることが分かります。
この例では、水平方向の変化を重視するフィルタを利用しましたが、同じ原理で、垂直方向を重視するフィルタや斜めを重視するフィルタなどを適用することも可能です。