前回述べた一次微分フィルタは、画素同士の輝度の変化が大きいところを捕らえるのに向いていました。
ただ、輝度の変化が大きいところが必ずしも、輪郭を示しているわけではない場合があります。
そういう場合、一次微分だけでなく、二次微分を使うといい場合があります。
その基礎的な原理について理解しておきましょう。
一次微分と比べた、二次微分の幾何学的な意味
たとえば、陰影のあるりんごの画像を思い浮かべてみてください。
輝度変化に基づくエッジ抽出ロジックだと、光の当たっていると影の部分がエッジとして抽出されてしまうことになります。
そこで、隣り合った画素の輝度変化だけでなく、周りに比べて「その変化の程度」が大きいところを抽出するというロジックが考えられます。
隣り合った画素同士の変化量を一次部分だとすると、その変化の程度というのはそれをさらに微分すること、すなわち2次微分することによって求まるといえます。
(速度をさらに微分すると加速度になる、あの関係を思い出すと、イメージしやすいと思います)
Laplacianとは2次微分の意味です。
これらの幾何学的な意味をイメージするために、隣り合った画素の変化の差分を考えてみましょう。
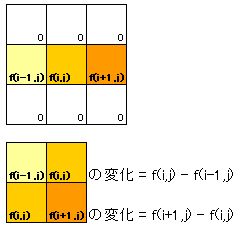
これらの2次微分 = 上記の各変化の差分 = f(i,j) – f(i-1,j) – (f(i+1,j) – f(i,j)) = 2*f(i,j) – f(i-1,j) – f(i+1,j)
となります。これらを垂直方向、さらに斜め方向にも考えると、
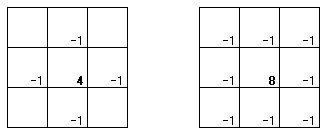
となるでしょう。
これらがそれぞれ、「4近傍Laplacianフィルタ」「8近傍Laplacianフィルタ」といわれるものになっていることが分かります。